A probabilistic model for interpreting strike-zone expansion

First, grab some data

To reach the goal stated above, I first grabbed every called strike and ball during the 2008 and 2014 seasons from my PITCHf/x database. This restricts us to cases where the home plate umpire has to make a decision between strike and ball. Also, pitches with missing horizontal (px) and vertical (pz) locations were thrown out (these are mostly preseason games anyway).

library(dplyr)
db <- src_sqlite("~/pitchfx/pitchRx.sqlite")
pitches <- tbl(db, "pitch") %>%
  select(px, pz, des, count, num, gameday_link) %>%
  filter(px != "NA" & pz != "NA") %>%
  filter(des %in% c("Called Strike", "Ball")) %>%
  # Create a 0-1 indicator for strike (the response)
  mutate(strike = as.numeric(des == "Called Strike"))

Some other important co-variates that we should include in our model are recorded on the at-bat level, so we join that information accordingly before executing the query and pulling the data into R.

atbats <- tbl(db, "atbat") %>%
  mutate(year = substr(date, 5L, -4L)) %>%
  select(stand, b_height, num, year, gameday_link) %>%
  filter(year %in% c("2008", "2014"))
# Join these 'tables' together into one table
tab <- left_join(x = pitches, y = atbats, 
                 by = c("gameday_link", "num"))
# Execute the database query and bring data into R
dat <- collect(tab)

To keep mgcv happy, any character variables that we put in the model need to be coerced into factors:

dat$stand <- factor(dat$stand)
dat$count <- factor(dat$count)
dat$year <- factor(dat$year)

The Model

In addition to batter stance, the pitch count can also affect the likelihood of a called strike. For this reason, I fit a model with a different surface (the surface estimates the probability of a called strike) for each unique combination of stand, year, and count (that gives us 2 x 2 x 12 = 48 surfaces)! Note that since I am using interaction(stand, year, count) for both intercept and ‘by’ variables, both the ‘average’ height and ‘wiggliness’ of each surface are allowed to be different. If you’d like to know more details about gams, the help(gam.models) is a decent place to start.

library(mgcv)
m <- bam(strike ~ interaction(stand, year, count) +
            s(px, pz, by = interaction(stand, year, count)),
          data = dat, family = binomial(link = 'logit'))

Results

Since there are so many coefficients, I’ll spare you the output of summary(m1). In short, the coefficients for the smoothed term are all highly significant while the coefficients for the intercept term are significant when the number of balls is 0 or 1. More interestingly, we can estimate the probability of a called strike at any arbitrary location and study how this estimate changes given different co-variate values. For example, the probability of a called strike for a knee-high first pitch thrown in middle of plate to a left hander in 2008 is 0.37, but in 2014, that probability increases 0.86. In other words, for this example, umpires were 2.3 times more likely to call a strike in 2014 than in 2008.

df <- data.frame(px = c(0, 0), pz = c(1.7, 1.7), 
                 stand = c("L", "L"), count = c("0-0", "0-0"), 
                 year = c("2008", "2014"))
predict(m, newdata = df, type = "response")

##         1         2 
## 0.3707173 0.8617872 

The code and plot below is meant to extend this type of comparison in probabilities for every possible count. More specifically, the y-axis represents the probability of a called strike for a knee-high first pitch thrown in middle of plate to a left hander and x-axis has the various pitch counts. The text in the middle of the plot represents how many times more likely a called strike is when going from 2008 to 2014. The plot indicates that as the number of strikes increases, the probability of a called strike decreases and the odds for a called strike in 2014 (against a called strike in 2008) increases. One other interesting thing here is that the number of strikes in a three ball count had a tremendous affect in 2008, but it no longer has much impact.

counts <- rep(sort(unique(dat$count)), each = 2)
n <- length(counts)
df2 <- data.frame(px = rep(0, n), pz = rep(1.7, n), 
                  stand = rep("L", n), count = counts,
                  year = rep(c("2008", "2014"), n/2))
df2$prob <- as.numeric(predict(m, newdata = df2, 
                               type = "response"))
times <- with(df2, tapply(prob, INDEX = count, 
                          function(x) round(x[2]/x[1], 1)))
y <- with(df2, tapply(prob, INDEX = count, 
                      function(x) (x[2] + x[1])/2))
df3 <- data.frame(count = row.names(times), 
                  times = times, y = y)
library(ggplot2)
ggplot() + geom_point(data = df2, 
                      aes(y = prob, x = count, color = year)) +
  geom_text(data = df3, 
            aes(y = y, x = count, label = times))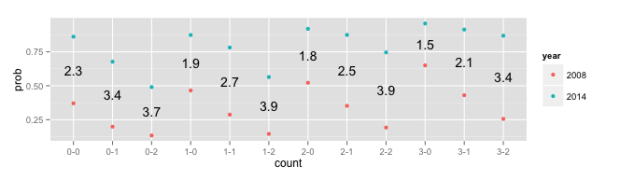

Instead of restricting focus to a single location, strikeFX provides a convenient way to plot entire surfaces as well as the difference between surfaces. In the function call below, we take each 2008 surface and subtract the corresponding 2014 surface. This reduces our original 48 surfaces to 24 differenced surfaces. These differenced surfaces estimate the difference in probability of a called strike in 2008 versus 2014 (in various scenarios). Notice how the difference in probability for a pitch at the knees is mostly around -0.5 (which is consistent with the earlier plot).

strikeFX(dat, model = m, density1 = list(year = "2008"),
          density2 = list(year = "2014"), 
          layer = facet_grid(count ~ stand)) +
      coord_equal()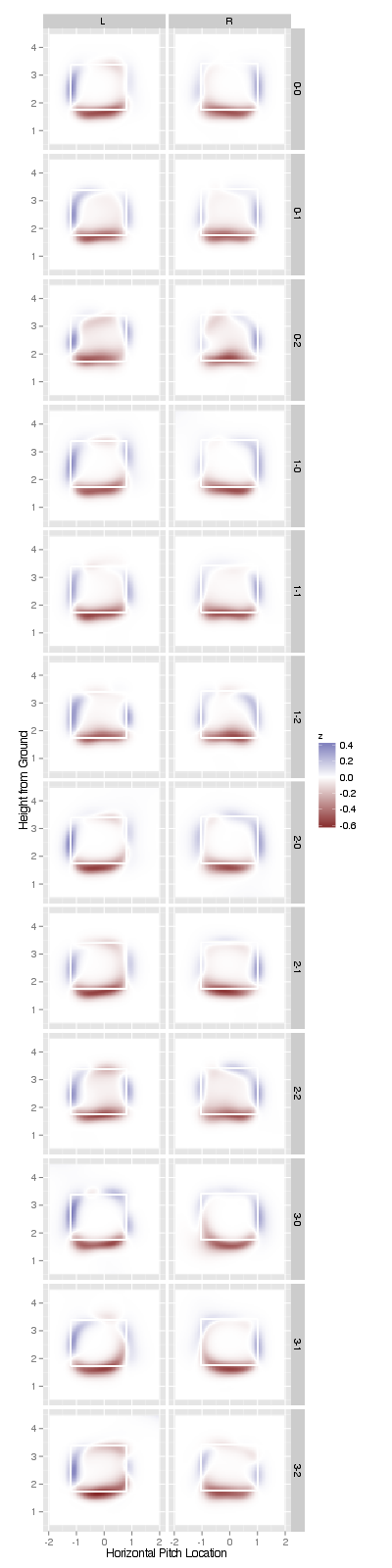

Not only are called strikes at the knees 2-4 times more likely in 2014, but called strikes up-and-in or up-and-away are much less likely nowadays. I also find it interesting that in two-strike counts, the probability of a called strike in 2014 is more likely for a large portion of the strike-zone (most noticeably at the top of the strike-zone).

Aside on technical issues

In the past, I’ve used bam to fit models in parallel with this much data on my local machine following Brian’s advice. I got tired of it hogging my machine’s resources for many hours at a time, so I decided to look into using DigitalOcean to run these jobs on a cloud server (students can get $100 in free credit). To be honest, it was painful to set up, but it should pay off in the long run. Part of the problem is that Ubuntu wants to kill R when it eats up too much memory. There must be a way to prevent the system from killing R, but I’m no Linux guru, so my solution was to scale the server up to 256GB of RAM just to fit the model.